English Version: Introduction to Spherical Harmonics
尽量不用各种术语来讲清楚SH(Spherical Harmonics)系数,以及SH在简单光照描述上的应用。 科普向。
SH,球谐函数,归根到底只是一组基函数,至于这组基函数是怎么来的,不管他。
其实大家小学二年级学过泰勒展开和傅里叶变换的话,对基函数应该是非常了解的。
比如多项式基函数:
$ y_{0} = 1 $
$ y_{1} = x$
$ y_{2} = x^2$
$ y_{3} = x^3$
….
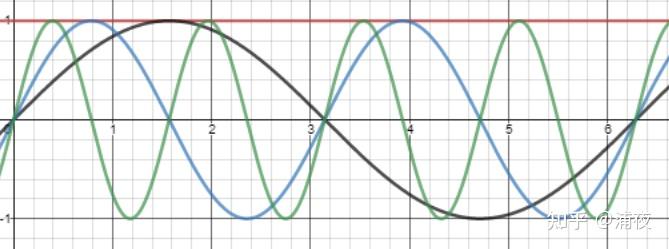
比如三角函数基函数:
$y_{0} = 1 $
$y_{1} = sin(x)$
$y_{2} = sin(2x)$
$y_{3} = sin(4x)$
….
或者也可以随便乱写一个基函数:
$y_{0} = 555$
$y_{1} = \frac{1}{x} + tan(x)$
$y_{2} = x^3 - 666$
$y_{3} = sin(4x)$
….
有了基函数,就可以把任意一个函数,描述成几个基函数的加权和了。
例如
$y \approx 0.1 y_0 + 0.3 y_1 + 0.8 y_2 + 0.001 y_3+…$
这时候,就相当于是把一个原始函数
$y = f(x)$
变成了一组系数:
0.1, 0.3, 0.8, 0.001, …
一般的,能用的基函数个数越多,表达能力就越强。
本质上是一个有损压缩。有点像个密码本,你一本我一本,上面写了基函数的定义,这样传密码的时候只要传几个系数就可以了,系数传到我这儿,我能复原出y = f(x),只是没那么准确了。
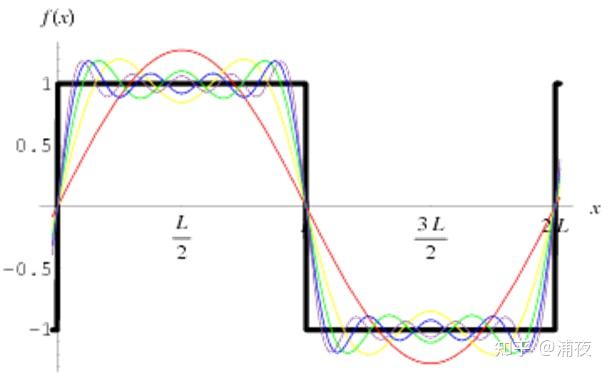
以下面这个方波函数为例,黑色的这个方波函数不能准确的用几个正弦基函数的加权描述,但是当基函数用的个数越多,跟方波函数本身也就越接近。
这里用的是二维直角坐标系,拓展到极坐标系的基函数也可以随便举个例子:
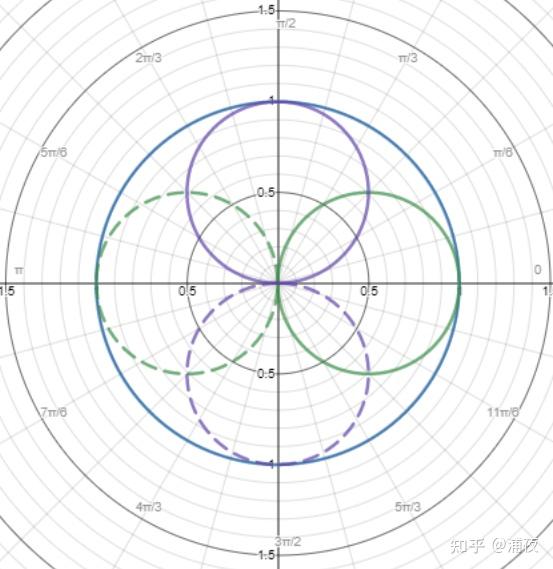
例如:
$ r_0 = 1 $ (蓝色)
$r_1 = cos θ $ (绿色)
$r_2 = sin θ$ (紫色)
$r3 = …$
三维也是一样的,三维直角坐标系的函数可能长这样
直角坐标系的基长这样
$z_0 = f_0(x, y) $
$z_1 = f_1(x, y) $
$z_2 = f_2(x, y) $
…
对应的,三维直角坐标系也可以拓展到三维球面坐标系。
而三维球面坐标系上的函数画出来可能是这样的:
不用距离而是用颜色来描述的话就可能是这样
球面坐标系的基长这样:
$r_0 = f_0(θ,φ) $
$r_1 = f_1(θ,φ) $
$r_2 = f_2(θ,φ) $
…
最有名的球面基函数就是球谐函数了。球谐函数有很多很好的性质,比如正交性,旋转不变性(这边就不介绍了)。正交性说明每个基函数都是独立的,每个基函数都不能用别的基函数加权得到。
SH的基函数长这样(其中蓝色表示正数,黄色表示负数),一般尝试了解过SH的同学都见过这个图:
表达式长这样:
第一次看完表达式之后的心情一般如下
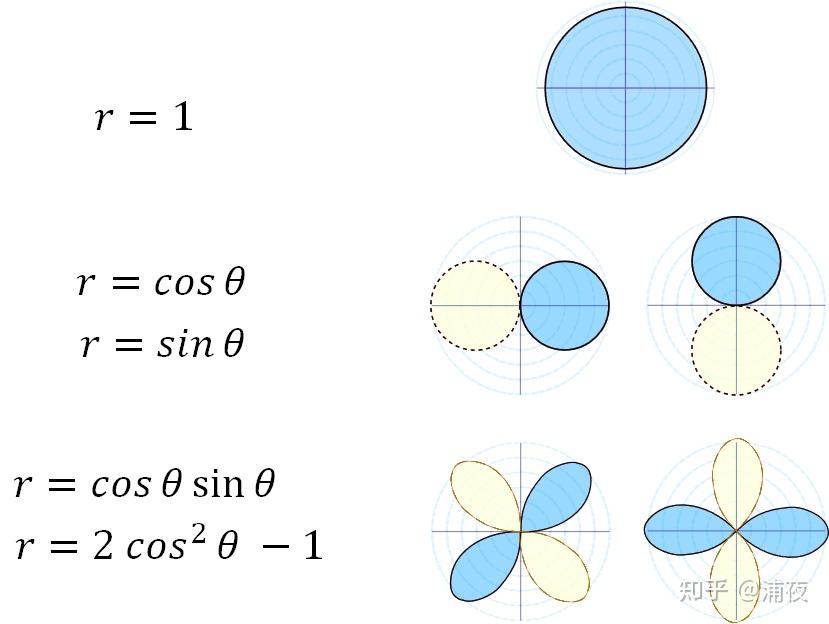
其实退化到二维来看,还是很简单的,二维的SH差不多长这样,蓝色表示正数,黄色表示负数:
(具体系数不太准确仅用于示意…)
像这样是不是就特别简单了,em,看这个波瓣长得似乎有点三维SH的意思了嘛。
(可以思考一个小问题:为啥二维情况下第三排的基函数只有cos平方,没有sin平方呢?)
假如有一个极坐标的函数长这样:
他可以表示为
$r = 0.5 + 0.1 cos θ + 0.07 sin θ + 0.05 cos θ sin θ + 0.3(2cos^2θ - 1)$
只记系数,这个函数就压缩为了:
0.5, 0.1, 0.07, 0.05, 0.3
回到三维的情况这几个数字其实就是SH系数啦。
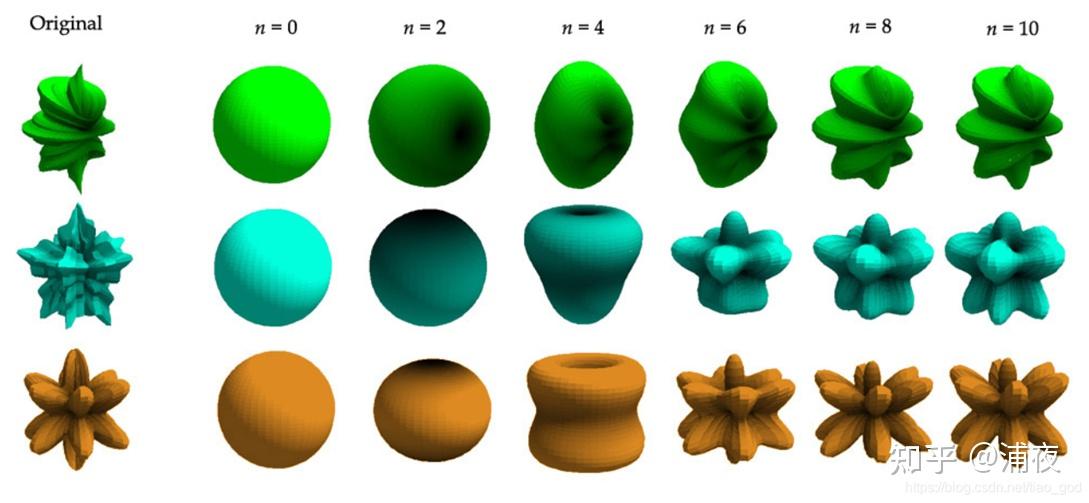
当SH的系数用的越多,那么表达能力就越强,跟原始的函数就越接近
当用来描述不同方向光照的SH基函数我们一般用到二阶或者三阶,二阶是4个系数:
拓展到rgb,就是4 * 3 = 12个系数
三阶是9个系数:
拓展到rgb,就是9 * 3 = 27个系数
空间中的每个Probe带一组SH系数,就可以描述这个位置的大致光照情况了。
为啥不用更高阶的SH?一方面是因为更多的系数会带来更大的存储压力、计算压力,而一般描述变化比较平滑的环境漫反射部分,用3阶SH就足够了;另一方面则是因为SH的物理含义不是特别好理解,高阶SH容易出现各种花式Artifact,美术同学一般都会认为这种表现属于bug。
那有没有更直观物理含义更好理解的基函数的?也有的,比如SG




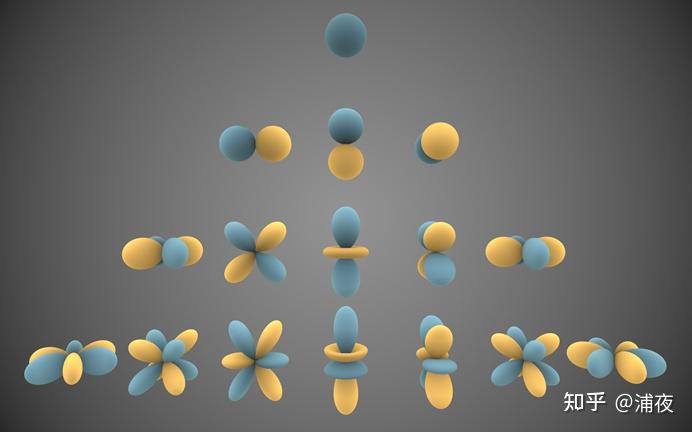
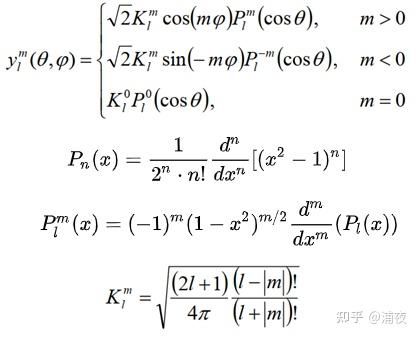


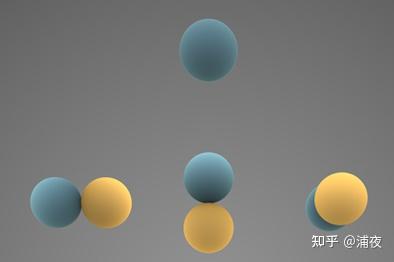


Comments powered by Disqus.