This article is still an informative introduction, presenting a new spherical basis function and its application in lighting description. Recommended prerequisite reading:
Introduction to Spherical Harmonics
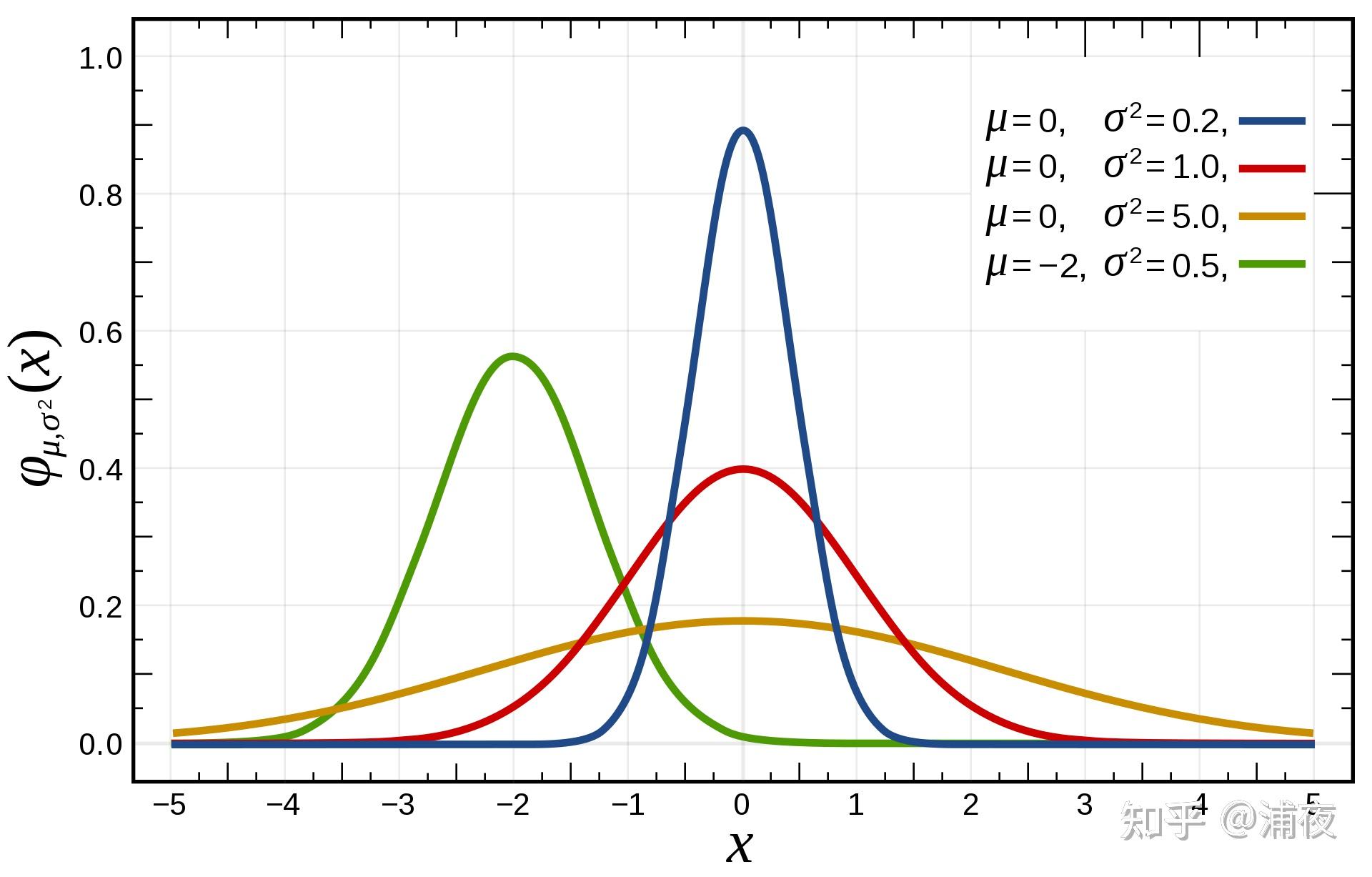
If you have studied probability and statistics in the third grade of elementary school, you must be very familiar with the normal distribution or Gaussian distribution.
\[g(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{(\frac{-(x-\mu)^2}{2\sigma^2})}\]Extending to Spherical Coordinates is quite straightforward. Compared to the SH formula, the Spherical Gaussian formula is much simpler, taking the form of:
\[G(v; \mu,\lambda,a) = ae^{\lambda(\mu\cdot v - 1)}\]The image in 2D Cartesian Coordinates looks like this.
The physical meaning of the parameters is also easy to understand. a represents the size of the lobe, μ represents the central direction of the lobe, and λ represents the fatness of the lobe.
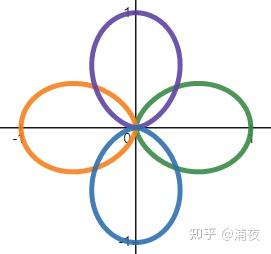
Compared to the fixed SH basis function, SG has an extremely high degree of freedom: the number of basis functions used, how they are distributed, and how fat they are can all be arbitrary. Of course, this also places higher demands on the person designing the basis function, otherwise it may be costly and the effect may not be good. Like other basis functions, the more basis functions used, the stronger the expressive power. Generally, a set of SG basis functions contains multiple basis functions in different directions, such as this: 
SG basis functions are also appropriate for describing specular reflection because they resemble the results of BRDF calculations.
With so many advantages, SG is simple and easy to understand, and it doesn’t have the messy artifacts of higher-order SH. So, who would still use SH?
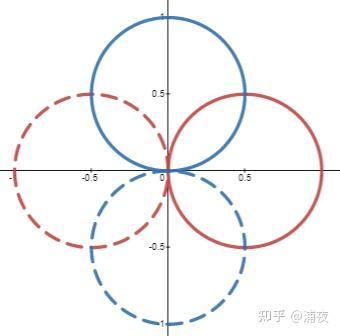
However, SH has many strengths that SG lacks, such as Orthogonality and Rotational Invariance. Let’s illustrate Rotational Invariance with an example:
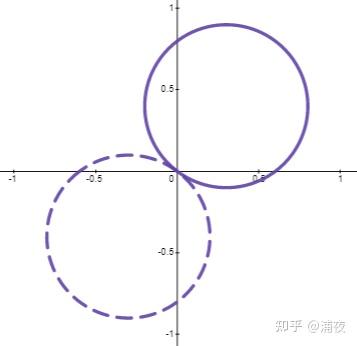
Suppose we have two SH basis functions (blue and red), and we want to use these two basis functions to describe another function with the same shape as the basis functions (purple)
It’s incredibly easy to obtain the result using the weighted sum of two basis functions (coefficients are 0.8 and 0.6)
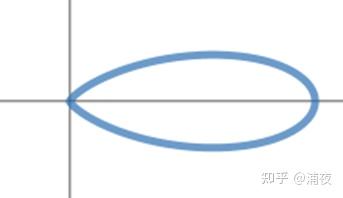
What if we want to use two SG basis functions (red and blue) to describe the black function result?
However, no matter how the coefficients are adjusted, the target characteristics cannot be approached. The closest reconstruction result with the coefficients is the purple heart shape shown in the image below.
When applied to actual specular calculations, it is found that SG cannot maintain the shape of the specular lobe very well. The shape of the specular lobe in the direction of the basis function definition can be maintained relatively well, but if the direction is between the angles of several basis functions, the shape of the specular lobe will be more scattered.
The”Order:”1886 uses SG to describe the specular, with each basis function using a set of Lightmaps. It seems that the problem of specular deformation is not very obvious.
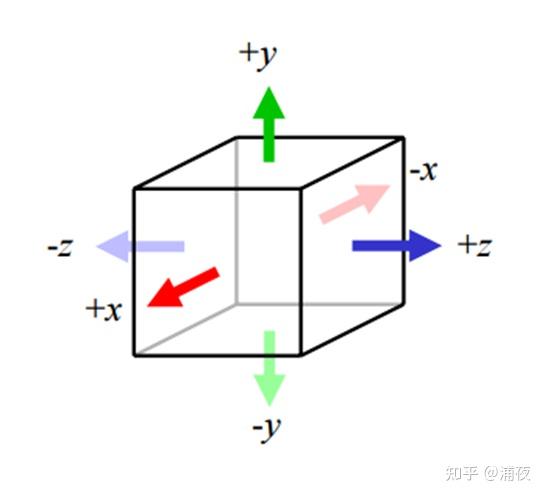
In fact, when it comes to describing diffuse lighting, SG is not commonly seen. Ambient Cube (also known as HL2) is more popular among artists, with one intensity description for each direction:
In 2D Cartesian Coordinates, it probably looks like this when degenerated.
The function shape and properties are very similar to SG (although the expressions are different)
Why is Ambient Cube more popular among artists? Because it is very easy to understand its physical meaning, and you can adjust it wherever you want. Developers who use SH basis functions to describe diffuse reflections have encountered such complaints: Why can’t the negative y direction be darker? It should be completely black at the bottom! But with Ambient Cube, this problem doesn’t exist. If you want to make a certain direction pure black, just change the corresponding direction coefficient to 0.
When comparing the number of coefficients, the commonly used ones are: 2nd order SH has 4 coefficients, Ambient Cube has 6 coefficients, and 3rd order SH has 9 coefficients.
Reference links:
https://blog.selfshadow.com/publications/s2015-Shading-course/rad/s2015_pbs_rad_slides.pdf https://mynameismjp.wordpress.com/2016/10/09/SG-series-part-2-spherical-gaussians-101/





Comments powered by Disqus.