本篇还是比较科普向,介绍了一种新的球面基函数和在光照描述上的应用。前置阅读:
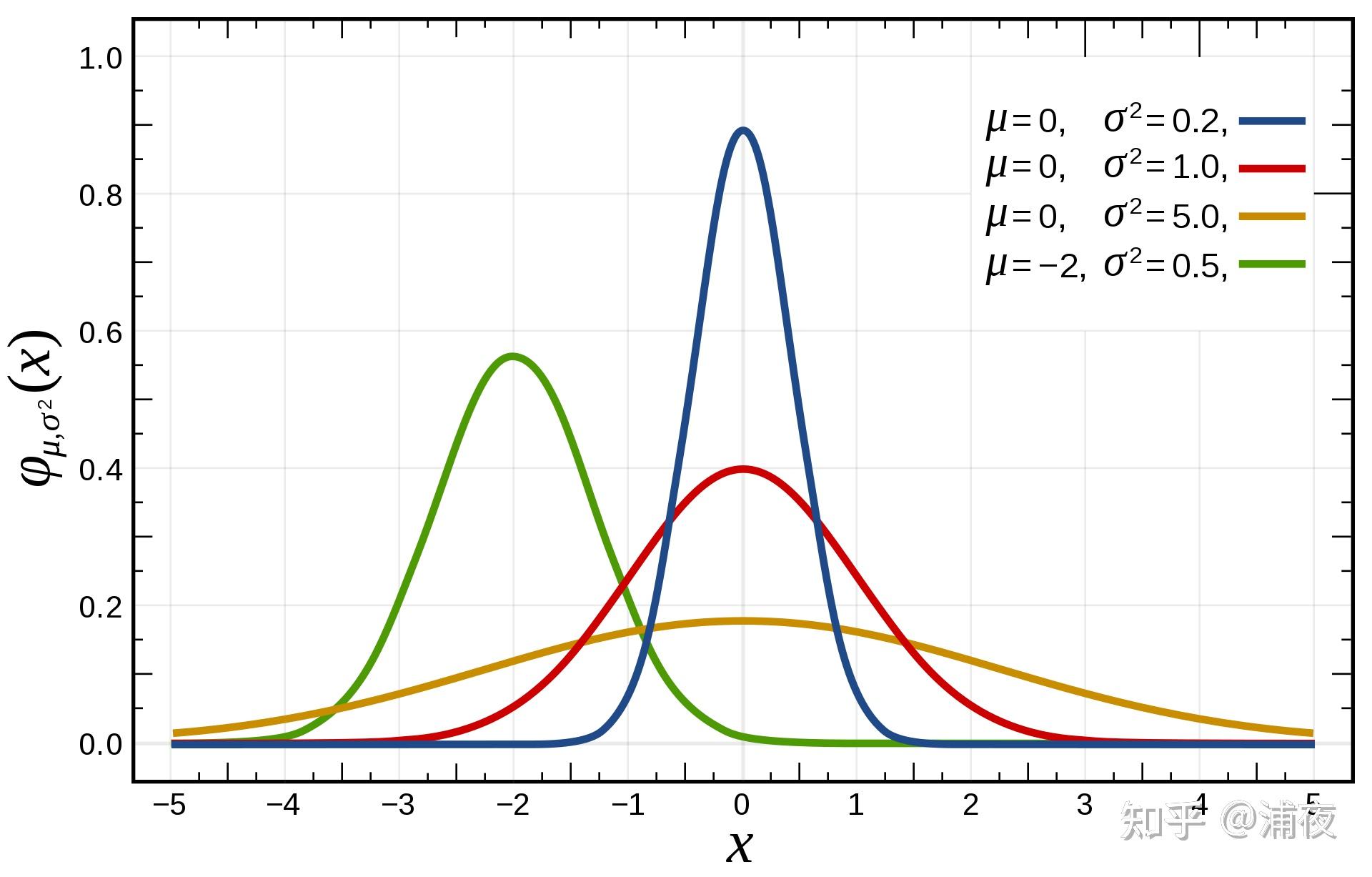
大家小学三年级学过概率和统计的话,对正态分布或者高斯分布一定非常了解
\[g(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{(\frac{-(x-\mu)^2}{2\sigma^2})}\]拓展到球面也很简单。相比SH的公式,Spherical Gaussian的公式就简单的多了,形如
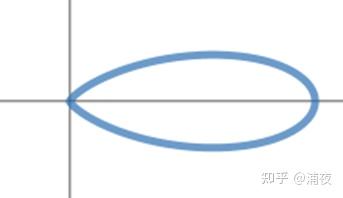
\[G(v; \mu,\lambda,a) = ae^{\lambda(\mu\cdot v - 1)}\]二维图像长得像这样
参数的物理含义也很好理解,a表示波瓣的大小,μ表示波瓣的中心方向,λ表示波瓣的胖瘦
和SH定死的基函数相比,SG的特点就是自由度极高:基函数用几个、怎么分布、胖瘦如何,都随意。当然这也对设计基函数的人提出了更高的要求,否则可能花费很多效果又不好。和别的基函数一样,用的基函数个数越多,表达能力就越强。一般一套SG基函数包含多个不同方向的基函数,例如这样:
SG基函数和镜面反射计算的结果又比较接近,因此可以用来描述高光。
SG有这么多好处,又简单又好理解的,还没有高阶SH那些乱七八糟的Artifact,那谁还用SH啊。
然而SH也有很多长处是SG没有的,比如SH除了正交性还有旋转不变性。还是举个例子来说明:
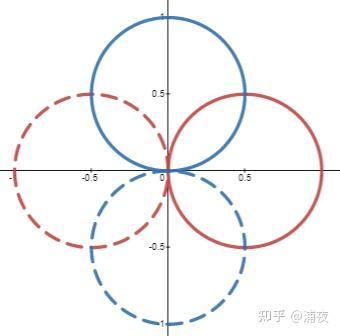
假如有两个SH基函数(蓝色和红色),我想要用这两个基函数描述另一个和基函数形状一样的函数(紫色)
很方便的可以用两个基函数的加权得到(系数是0.8和0.6)
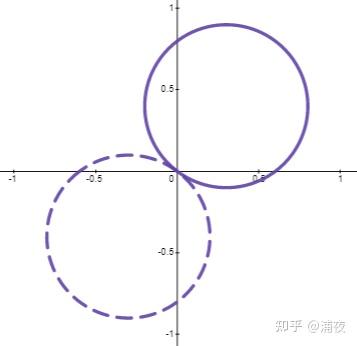
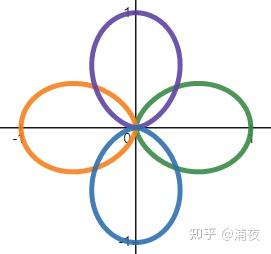
那假如是SG的两个基函数(红色和蓝色)想描述黑色的这个函数结果呢
却发现怎么调整系数,都接近不了这个目标性状。最接近的系数的重建结果是下图紫色爱心形。
反馈到实际高光计算上,就会发现SG不能很好地保持高光形状。基函数定义方向上的高光形状能保持的比较好,但如果位置在几个基函数的角度之间,高光形状就会比较散了。
教团的文章 就是使用SG来描述高光,每个基函数都用一套Lightmap。看起来高光变形的问题应该也不明显。
虽然我觉得这个思路过分奢侈,不过还是很有启发性的。
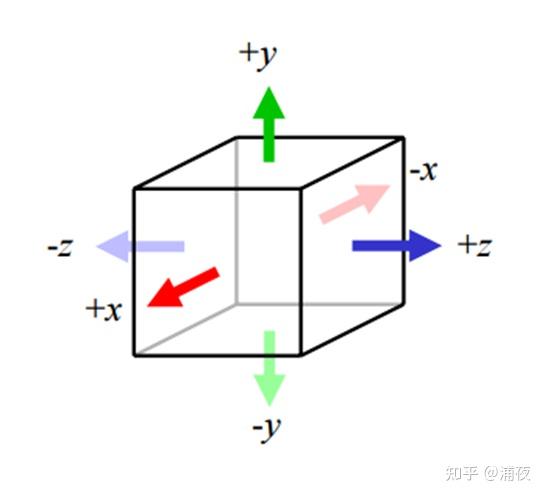
其实真正描述光照漫反射,SG倒不多见,比较受美术欢迎的是Ambient Cube(也叫HL2),每个方向一个强度描述:
退化到二维大概长这样
函数形状和性质与SG非常相像(表达式其实不一样)
为什么受美术欢迎呢?因为它的物理含义非常好理解,哪里想改调哪里。用SH的基函数描述漫反射的同学多多少少碰到过这样的抱怨:y方向怎么就黑不下来呢!底下应该是全黑的啊!但ambient cube就不会了,想要把某个方向改成纯黑,只要把对应方向的系数改成0就行了。
从系数个数上来对比,一般常用的是这几种:二阶SH是4个系数,AmbientCube是6个系数,三阶SH是9个系数。
参考链接:
https://blog.selfshadow.com/publications/s2015-shading-course/rad/s2015_pbs_rad_slides.pdf https://mynameismjp.wordpress.com/2016/10/09/sg-series-part-2-spherical-gaussians-101/







Comments powered by Disqus.